Sistemas Lineares Em 3 Passos + Resumo Com Exemplos! – Beduka – Sistemas Lineares Em 3 Passos + Resumo Com Exemplos!
-Beduka: Dominar sistemas lineares pode parecer um desafio, mas com a abordagem certa, a solução se torna acessível. Este guia descomplica o processo, apresentando métodos eficazes de resolução passo a passo, ilustrados com exemplos práticos que vão desde problemas de mistura até aplicações em circuitos elétricos e trajetórias de projéteis.
Prepare-se para entender a lógica por trás dessas equações e aplicar seus conhecimentos em situações reais!
Vamos explorar os conceitos fundamentais de sistemas lineares, diferenciando sistemas consistentes e inconsistentes. Aprenderemos métodos de resolução como substituição e adição, comparando suas vantagens e desvantagens. Através de exemplos detalhados e aplicações práticas, você desenvolverá a habilidade de modelar e resolver problemas complexos utilizando sistemas lineares, consolidando seu aprendizado com um resumo conciso e eficiente.
Introdução a Sistemas Lineares

Sistemas lineares são um conjunto de equações lineares que compartilham as mesmas variáveis. A solução de um sistema linear consiste em encontrar os valores dessas variáveis que satisfazem simultaneamente todas as equações do sistema. A compreensão de sistemas lineares é fundamental em diversas áreas, desde a matemática pura até aplicações práticas em engenharia, economia e ciência da computação.Um sistema linear é composto por equações da forma a1x 1 + a 2x 2 + …
+ a nx n = b , onde ai são constantes (coeficientes), xi são as variáveis e b é uma constante (termo independente). A linearidade se caracteriza pela ausência de termos com potências superiores a 1 nas variáveis e pela ausência de produtos entre as variáveis.
Sistemas Lineares Consistentes e Inconsistentes
Um sistema linear é considerado consistente se possui pelo menos uma solução, ou seja, se existe pelo menos um conjunto de valores para as variáveis que satisfazem todas as equações simultaneamente. Caso contrário, o sistema é inconsistente, significando que não existe solução que satisfaça todas as equações ao mesmo tempo. A consistência ou inconsistência de um sistema pode ser determinada através de métodos de resolução como a eliminação de Gauss ou a regra de Cramer.
Um sistema consistente pode ter uma única solução (sistema determinado) ou infinitas soluções (sistema indeterminado).
Exemplos de Problemas Modelados por Sistemas Lineares
Sistemas lineares são ferramentas poderosas para modelar uma variedade de problemas do mundo real. A capacidade de representar relações lineares entre diferentes variáveis permite a resolução de problemas complexos de forma sistemática.
| Problema | Equações | Variáveis | Solução |
|---|---|---|---|
| Mistura de soluções químicas | x + y = 100 0.1x + 0.2y = 18 |
x (litros de solução a 10%), y (litros de solução a 20%) | x = 40, y = 60 |
| Determinação de preços de produtos | 2x + y = 25 x + 3y = 30 |
x (preço do produto A), y (preço do produto B) | x = 7.5, y = 10 |
| Distribuição de tarefas em uma equipe | x + y + z = 100 2x + y = 60 x + 3z = 70 |
x (tarefas do membro A), y (tarefas do membro B), z (tarefas do membro C) | x = 20, y = 20, z = 60 |
| Análise de circuitos elétricos (Lei de Kirchhoff) | i1 + i2 = i3 R1i1 + R2i2 = V |
i1, i2, i3 (correntes), R1, R2 (resistências), V (tensão) | Depende dos valores de R1, R2 e V. |
Métodos de Resolução de Sistemas Lineares em 3 Passos
Resolver sistemas lineares é uma habilidade fundamental em diversas áreas, como engenharia, economia e ciência da computação. Existem diferentes métodos para encontrar a solução, e a escolha do método mais adequado depende da complexidade do sistema. Neste tópico, exploraremos dois métodos comuns: o método de substituição e o método da adição (ou eliminação). Ambos são eficazes, porém apresentam vantagens e desvantagens que serão discutidas posteriormente.
Método de Substituição
O método de substituição consiste em isolar uma variável em uma das equações e substituí-la na outra equação, reduzindo assim o número de variáveis e simplificando o processo de resolução. Vamos analisar sua aplicação em sistemas 2×2 e 3×3.
Sistema Linear 2×2:
Considere o sistema:
x + y = 5
x – y = 1
- Isolar uma variável: Da primeira equação, podemos isolar x: x = 5 – y.
- Substituir: Substituímos x = 5 – y na segunda equação: (5 – y) – y = 1.
- Resolver: Simplificando a equação, obtemos 5 – 2y = 1, logo 2y = 4, e y = 2. Substituindo y = 2 na equação x = 5 – y, encontramos x = 5 – 2 = 3. Portanto, a solução é x = 3 e y = 2.
Sistema Linear 3×3:
Considere o sistema:
x + y + z = 6
x – y + z = 2
x + y – z = 0
- Isolar uma variável: Isolando x na primeira equação: x = 6 – y – z.
- Substituir: Substituímos x na segunda e terceira equações: (6 – y – z)
y + z = 2 e (6 – y – z) + y – z = 0.
- Resolver: Simplificando as equações, obtemos: 6 – 2y = 2 e 6 – 2z = 0. Resolvendo essas equações, encontramos y = 2 e z = 3. Substituindo y e z na equação x = 6 – y – z, encontramos x = 6 – 2 – 3 = 1. Portanto, a solução é x = 1, y = 2 e z = 3.
Método da Adição (Eliminação)
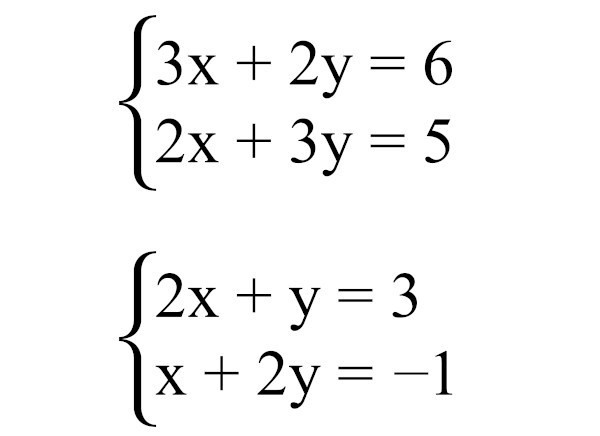
O método da adição consiste em somar ou subtrair as equações do sistema de forma a eliminar uma das variáveis. Este método é particularmente útil quando as equações possuem coeficientes convenientes para a eliminação direta ou após multiplicação por constantes.
Sistema Linear 2×2:
Considere o sistema:
x + y = 5
x – y = 1
- Somar as equações: Somando as duas equações, eliminamos y: (x + y) + (x – y) = 5 + 1, resultando em 2x = 6, logo x = 3.
- Substituir: Substituindo x = 3 em qualquer uma das equações originais (por exemplo, x + y = 5), encontramos 3 + y = 5, logo y = 2.
- Solução: A solução é x = 3 e y = 2.
Sistema Linear 3×3:
Considere o sistema:
x + y + z = 6
x – y + z = 2
x + y – z = 0
- Somar equações para eliminar variáveis: Somando a primeira e a terceira equações, eliminamos z: 2x + 2y = 6, simplificando para x + y = 3.
- Combinar equações: Subtraindo a segunda equação da primeira, eliminamos x: 2y = 4, logo y = 2.
- Substituir e resolver: Substituindo y = 2 em x + y = 3, encontramos x = 1. Substituindo x = 1 e y = 2 na primeira equação original, encontramos z = 3. A solução é x = 1, y = 2 e z = 3.
Comparação dos Métodos
A escolha entre o método de substituição e o método da adição depende das características do sistema linear.
| Método | Vantagens | Desvantagens |
|---|---|---|
| Substituição | Simples para sistemas pequenos; fácil de entender e aplicar. | Pode ser trabalhoso para sistemas maiores e com coeficientes fracionários; propenso a erros de cálculo em sistemas complexos. |
| Adição (Eliminação) | Eficiente para sistemas maiores; menos propenso a erros de cálculo em sistemas com coeficientes inteiros. | Pode ser mais complexo de aplicar em sistemas com coeficientes fracionários; requer habilidade em manipular equações. |
Aplicações e Exemplos de Sistemas Lineares: Sistemas Lineares Em 3 Passos + Resumo Com Exemplos! – Beduka

Sistemas lineares são ferramentas matemáticas poderosas com aplicações em diversas áreas, desde a química e engenharia elétrica até a física e a economia. Sua capacidade de modelar relações entre variáveis de forma concisa e eficiente os torna essenciais na resolução de problemas complexos. Nesta seção, exploraremos exemplos práticos em diferentes contextos, demonstrando a versatilidade e a importância dos sistemas lineares na resolução de problemas reais.
Exemplo de Problema de Mistura, Sistemas Lineares Em 3 Passos + Resumo Com Exemplos! – Beduka
Um problema clássico que ilustra a aplicação de sistemas lineares é o de misturas. Imagine que temos dois tipos de soluções de ácido sulfúrico: uma solução A com 20% de ácido e outra solução B com 60% de ácido. Desejamos obter 100 litros de uma solução C com 30% de ácido, misturando quantidades adequadas de A e B. Podemos modelar esse problema usando um sistema linear.
Sejam x a quantidade (em litros) da solução A e y a quantidade (em litros) da solução B. O sistema linear que representa o problema é:x + y = 100 (equação da quantidade total)
20x + 0.60y = 0.30(100) (equação da concentração de ácido)
Resolvendo este sistema, por exemplo, pelo método da substituição ou eliminação, encontramos x = 50 litros e y = 50 litros. Portanto, para obter a solução desejada, devemos misturar 50 litros da solução A com 50 litros da solução B.
Exemplo de Problema de Circuitos Elétricos
Em circuitos elétricos, a Lei de Ohm e as leis de Kirchhoff fornecem as equações necessárias para modelar o comportamento do circuito usando sistemas lineares. Considere um circuito simples com duas resistências, R1 e R2, conectadas em série a uma fonte de tensão V. A corrente I que flui pelo circuito pode ser calculada usando a Lei de Ohm: V = I(R1 + R2).
Se adicionarmos mais componentes e ramificações ao circuito, a análise se torna mais complexa, mas ainda pode ser representada por um sistema linear de equações, onde as incógnitas são as correntes em cada ramo do circuito. A resolução desse sistema fornece as correntes em cada parte do circuito.
Exemplo de Trajetória de um Projétil

A trajetória de um projétil lançado com uma velocidade inicial v0 e um ângulo θ em relação à horizontal pode ser modelada usando equações de movimento. Considerando a resistência do ar desprezível, as equações são:x = v0
- cos(θ)
- t
y = v0
- sen(θ)
- t – (1/2)gt²
onde x e y são as coordenadas do projétil, t é o tempo, e g é a aceleração da gravidade. Para determinar a trajetória, precisamos resolver este sistema de equações para x e y em função de t. Podemos encontrar, por exemplo, o tempo de voo e o alcance máximo do projétil a partir da solução deste sistema.
A modelagem matemática, como a utilização de sistemas lineares para descrever a trajetória de um projétil, é fundamental para a compreensão e a previsão do comportamento de sistemas físicos. Ela permite a análise quantitativa de fenômenos complexos e a otimização de projetos em diversas áreas da engenharia e da ciência.
Conseguimos desvendar o mundo dos sistemas lineares! De conceitos básicos a métodos de resolução eficazes, exploramos diversas aplicações práticas, mostrando como esses sistemas são ferramentas essenciais para modelar e solucionar problemas em diferentes áreas. Com a prática e a compreensão dos métodos de substituição e adição, você estará pronto para enfrentar desafios mais complexos, aplicando seus conhecimentos em situações reais com confiança e precisão.
Lembre-se: a prática leva à perfeição!

