Regra De Três Simples: Como Fazer, Exemplos, Questões – dominar essa ferramenta matemática é essencial para diversas áreas! Este guia descomplica a regra de três simples, mostrando, passo a passo, como resolver problemas, tanto diretos quanto inversos. De exemplos práticos do dia a dia a aplicações em áreas como física e finanças, você vai entender a lógica por trás dos cálculos e se tornar um mestre na resolução de problemas proporcionais.
Prepare-se para desvendar os segredos dessa técnica poderosa e eficiente!
Abordaremos os conceitos fundamentais, diferenciando a regra de três simples direta da inversa, e apresentaremos métodos práticos e eficazes para resolver uma variedade de problemas. Veremos exemplos detalhados, com explicações claras e concisas, para que você possa aplicar o aprendizado imediatamente. Além disso, exploraremos aplicações em diferentes contextos, mostrando a versatilidade dessa ferramenta matemática.
Conceitos Fundamentais da Regra de Três Simples: Regra De Três Simples: Como Fazer, Exemplos, Questões

A regra de três simples é uma ferramenta matemática fundamental utilizada para resolver problemas de proporcionalidade entre duas grandezas. Ela se baseia na relação constante entre essas grandezas, permitindo calcular um valor desconhecido a partir de três valores conhecidos. A compreensão de seus tipos e a capacidade de identificar a proporcionalidade são essenciais para sua aplicação eficaz.
Definição da Regra de Três Simples e seus Tipos
A regra de três simples estabelece uma relação de proporcionalidade entre duas grandezas. Existem dois tipos principais: direta e inversa. Na regra de três simples direta, o aumento de uma grandeza implica no aumento proporcional da outra, e a diminuição de uma implica na diminuição proporcional da outra. Já na regra de três simples inversa, o aumento de uma grandeza implica na diminuição proporcional da outra, e vice-versa.
A chave para resolver corretamente um problema está em identificar corretamente qual tipo de proporcionalidade está em jogo.
Identificação do Tipo de Proporcionalidade
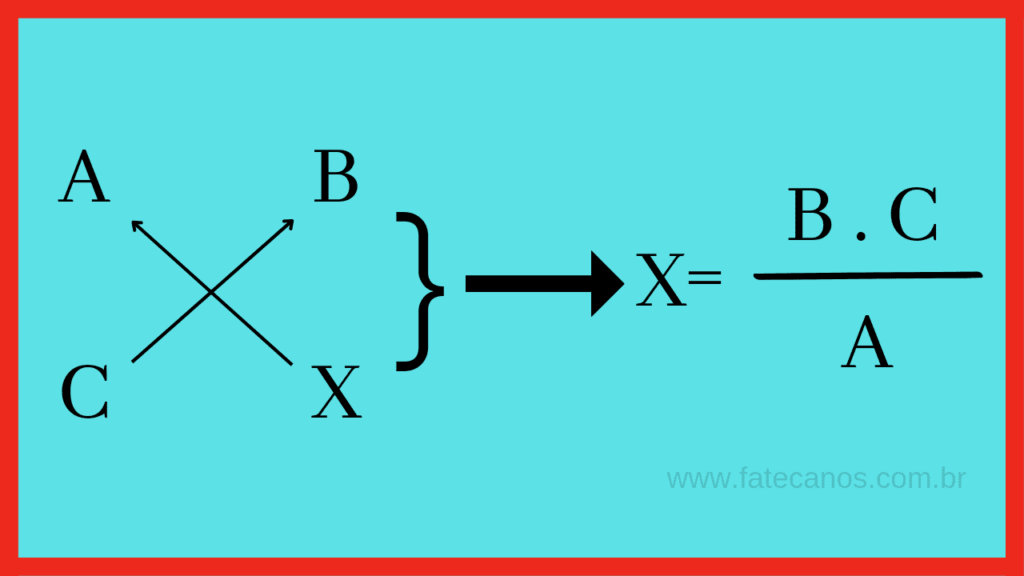
Para identificar o tipo de proporcionalidade, é crucial analisar a relação entre as grandezas envolvidas no problema. Pergunte-se: se uma grandeza aumenta, a outra também aumenta? Se sim, é uma proporcionalidade direta. Se uma grandeza aumenta e a outra diminui, é uma proporcionalidade inversa. Um exemplo prático: se o número de trabalhadores aumenta, o tempo necessário para concluir uma tarefa diminui (inversa).
Se o número de horas trabalhadas aumenta, o salário também aumenta (direta). A análise cuidadosa do enunciado do problema é fundamental para essa identificação.
Aplicações da Regra de Três Simples em Situações Cotidianas

A regra de três simples está presente em diversas situações do nosso dia a dia. Imagine calcular o preço total de uma compra com base no preço unitário e na quantidade de itens. Ou calcular a quantidade de combustível necessária para uma viagem, considerando a distância e o consumo do veículo. Outro exemplo seria determinar o tempo necessário para percorrer uma certa distância, conhecendo a velocidade e a distância.
A flexibilidade da regra de três simples a torna uma ferramenta poderosa para resolver problemas práticos em diversas áreas.
Comparação entre Regra de Três Simples Direta e Inversa, Regra De Três Simples: Como Fazer, Exemplos, Questões
A tabela abaixo compara as características da regra de três simples direta e inversa, com exemplos para ilustrar cada caso:
| Característica | Regra de Três Simples Direta | Regra de Três Simples Inversa | Exemplo |
|---|---|---|---|
| Relação entre grandezas | Diretamente proporcional | Inversamente proporcional | |
| Aumento de uma grandeza | Implica aumento da outra | Implica diminuição da outra | |
| Diminuição de uma grandeza | Implica diminuição da outra | Implica aumento da outra | |
| Exemplo 1 | Se 2 kg de arroz custam R$ 10,00, quanto custarão 5 kg? | Se 5 trabalhadores pintam uma casa em 3 dias, em quantos dias 15 trabalhadores pintarão a mesma casa? | Direta: aumento de kg implica aumento de preço; Inversa: aumento de trabalhadores implica diminuição de dias. |
| Exemplo 2 | Se um carro percorre 100 km com 10 litros de gasolina, quantos litros serão necessários para percorrer 300 km? | Se uma torneira enche um tanque em 6 horas, em quanto tempo 3 torneiras encherão o mesmo tanque? | Direta: aumento de distância implica aumento de consumo; Inversa: aumento de torneiras implica diminuição do tempo. |
Resolução de Problemas com Regra de Três Simples
A regra de três simples é uma ferramenta poderosa para resolver problemas que envolvem proporcionalidade entre duas ou mais grandezas. Dominar sua aplicação, tanto na forma direta quanto inversa, é fundamental para diversas áreas, desde o cálculo de porcentagens até a previsão de rendimentos. Neste segmento, detalharemos os métodos passo a passo para solucionar problemas de regra de três simples, tanto direta quanto inversa, fornecendo exemplos práticos para melhor compreensão.
Método Passo a Passo para Regra de Três Simples Direta
A regra de três simples direta é aplicada quando o aumento de uma grandeza implica no aumento proporcional de outra, ou quando a diminuição de uma implica na diminuição proporcional da outra. O método consiste em organizar os dados em uma tabela e realizar a multiplicação cruzada.
- Identifique as grandezas envolvidas e suas relações: Determine quais são as grandezas diretamente proporcionais no problema.
- Organize os dados em uma tabela: Crie uma tabela com duas colunas, representando as grandezas. Preencha com os valores conhecidos e a incógnita (geralmente representada por “x”).
- Efetue a multiplicação cruzada: Multiplique os valores na diagonal que contém a incógnita e divida pelo valor restante.
- Resolva a equação: Resolva a equação resultante para encontrar o valor da incógnita (x).
Método Passo a Passo para Regra de Três Simples Inversa
Na regra de três simples inversa, o aumento de uma grandeza implica na diminuição proporcional da outra, e vice-versa. A resolução difere da direta, exigindo uma inversão de um dos valores antes da multiplicação cruzada.
- Identifique as grandezas envolvidas e suas relações: Determine quais são as grandezas inversamente proporcionais.
- Organize os dados em uma tabela: Crie uma tabela com duas colunas, representando as grandezas. Preencha com os valores conhecidos e a incógnita (x).
- Inverter um dos valores: Inverte-se um dos valores de uma das grandezas antes de realizar a multiplicação cruzada. Normalmente, escolhe-se inverter o valor que está na mesma linha da incógnita.
- Efetue a multiplicação cruzada: Multiplique os valores na diagonal que contém a incógnita e divida pelo valor restante.
- Resolva a equação: Resolva a equação resultante para encontrar o valor da incógnita (x).
Resolução de Problemas com Grandezas Diretamente e Inversamente Proporcionais
A chave para resolver problemas de regra de três simples reside na correta identificação da relação entre as grandezas envolvidas. Se o aumento de uma grandeza causa o aumento proporcional da outra, a relação é direta. Se o aumento de uma causa a diminuição proporcional da outra, a relação é inversa. A escolha do método (direta ou inversa) depende dessa identificação.
Exemplos de Regra de Três Simples Direta
A seguir, cinco exemplos de problemas resolvidos utilizando a regra de três simples direta:
- Se 3 kg de maçãs custam R$ 12,00, quanto custarão 5 kg? Solução: (5 kg
– R$ 12,00) / 3 kg = R$ 20,00 - Um carro percorre 150 km com 10 litros de gasolina. Quantos quilômetros percorrerá com 25 litros? Solução: (25 L
– 150 km) / 10 L = 375 km - Se 4 operários constroem uma casa em 60 dias, em quantos dias 6 operários construirão a mesma casa? (Considerando a mesma produtividade individual) Solução: (4 operários
– 60 dias) / 6 operários = 40 dias - Uma máquina produz 100 peças em 2 horas. Quantas peças produzirá em 5 horas? Solução: (5 horas
– 100 peças) / 2 horas = 250 peças - Se 2 pintores pintam uma parede em 3 horas, em quanto tempo 6 pintores pintarão a mesma parede? Solução: (2 pintores
– 3 horas) / 6 pintores = 1 hora
Exemplos de Regra de Três Simples Inversa
Esses exemplos ilustram a aplicação da regra de três simples inversa:
- 10 operários constroem uma casa em 30 dias. Quantos dias serão necessários para 15 operários construírem a mesma casa? Solução: (10 operários
– 30 dias) / 15 operários = 20 dias - 5 máquinas produzem 1000 peças em 8 horas. Em quantas horas 10 máquinas produzirão as mesmas 1000 peças? Solução: (5 máquinas
– 8 horas) / 10 máquinas = 4 horas - Um ciclista percorre uma distância em 4 horas a uma velocidade de 20 km/h. Quanto tempo levará para percorrer a mesma distância a 25 km/h? Solução: (4 horas
– 20 km/h) / 25 km/h = 3,2 horas - 2 torneiras enchem uma piscina em 6 horas. Quanto tempo levarão 3 torneiras para encher a mesma piscina? Solução: (2 torneiras
– 6 horas) / 3 torneiras = 4 horas - Se 6 pessoas consomem um estoque de comida em 10 dias, em quantos dias 3 pessoas consumirão o mesmo estoque? Solução: (6 pessoas
– 10 dias) / 3 pessoas = 20 dias
Aplicações e Extensões da Regra de Três Simples
A regra de três simples, apesar de sua aparente simplicidade, é uma ferramenta poderosa com aplicações vastas e diversas em diferentes áreas do conhecimento. Sua capacidade de resolver problemas de proporcionalidade direta e inversa a torna essencial para a compreensão e resolução de problemas em contextos que vão além da matemática pura. Este texto explorará algumas dessas aplicações e extensões, incluindo sua comparação com outros métodos e a abordagem de problemas mais complexos.
Aplicações em Diferentes Áreas do Conhecimento
A regra de três simples encontra aplicações práticas em diversas áreas. Na física, por exemplo, é fundamental para resolver problemas envolvendo grandezas diretamente proporcionais, como velocidade, distância e tempo (v = d/t), ou inversamente proporcionais, como pressão e volume em um gás ideal (a pressão aumenta, o volume diminui, a temperatura constante). Em química, a estequiometria, que lida com as relações quantitativas entre reagentes e produtos em reações químicas, utiliza amplamente a regra de três para determinar quantidades de substâncias envolvidas.
No campo das finanças, cálculos de juros simples, porcentagens e conversão de moedas frequentemente se beneficiam da aplicação direta da regra de três. Em resumo, a versatilidade da regra de três simples permite sua aplicação em situações cotidianas e em contextos científicos complexos.
Comparação com Outros Métodos de Resolução de Problemas Proporcionais

Embora a regra de três simples seja eficiente para resolver problemas de proporcionalidade, outros métodos também podem ser utilizados, como a utilização de frações equivalentes ou a construção de gráficos. A escolha do método mais adequado depende da complexidade do problema e da familiaridade do resolvedor com as diferentes técnicas. A regra de três simples, por sua simplicidade e clareza, frequentemente se apresenta como a abordagem mais intuitiva e eficiente, especialmente para problemas com poucas variáveis.
A utilização de frações equivalentes, por sua vez, oferece uma perspectiva mais algébrica, enquanto gráficos podem ser úteis para visualizar a relação entre as grandezas. Cada método apresenta suas vantagens e desvantagens, sendo a escolha do melhor método uma questão de preferência e contexto.
Resolução de um Problema Complexo com Regra de Três Simples Direta e Inversa

Imagine uma fábrica que produz peças. A produção diária é diretamente proporcional ao número de funcionários e inversamente proporcional ao tempo de produção de cada peça. Se 10 funcionários produzem 1000 peças em 5 horas, quantas peças serão produzidas por 15 funcionários em 4 horas? Primeiro, resolvemos a proporcionalidade direta: (15 funcionários / 10 funcionários)
1000 peças = 1500 peças. Em seguida, a proporcionalidade inversa
1500 peças(5 horas / 4 horas) = 1875 peças. Portanto, 15 funcionários produziriam 1875 peças em 4 horas. Este exemplo demonstra a capacidade da regra de três simples de lidar com situações que envolvem múltiplas relações proporcionais.
Guia Passo a Passo para Resolução de um Problema de Regra de Três Composta
Para ilustrar a resolução de um problema de regra de três composta, vamos considerar o seguinte cenário: 5 pedreiros constroem uma parede de 10 metros de comprimento em 2 dias, trabalhando 8 horas por dia. Quantos dias serão necessários para 10 pedreiros construírem uma parede de 20 metros, trabalhando 6 horas por dia? Imagem 1: Tabela organizada com as grandezas. A imagem mostraria uma tabela com quatro colunas: Número de pedreiros, Comprimento da parede, Horas de trabalho por dia, e Número de dias.
As informações do problema seriam organizadas na tabela, separando as grandezas conhecidas das incógnitas. Imagem 2: Estabelecimento da proporção. A imagem ilustraria a montagem da proporção, mostrando como as grandezas são relacionadas. Por exemplo, o número de pedreiros é diretamente proporcional ao comprimento da parede e inversamente proporcional ao número de dias. As horas de trabalho por dia também são inversamente proporcionais ao número de dias.
Imagem 3: Cálculo da proporção. A imagem mostraria o cálculo passo a passo, com a multiplicação e divisão das grandezas, resultando na resposta final. A fórmula utilizada seria uma representação clara da proporção estabelecida na imagem anterior. Imagem 4: Resposta final. A imagem mostraria a resposta final, claramente destacada, indicando o número de dias necessários para a construção da parede nas novas condições.
Adaptação da Regra de Três Simples para Problemas com Mais de Duas Grandezas (Regra de Três Composta)
A regra de três composta estende o princípio da regra de três simples para problemas com mais de duas grandezas. Para resolver esses problemas, é crucial identificar as relações de proporcionalidade (direta ou inversa) entre cada grandeza e a grandeza incógnita. Em seguida, monta-se uma proporção, multiplicando as grandezas diretamente proporcionais ao numerador e as grandezas inversamente proporcionais ao denominador.
O exemplo da construção da parede, detalhado acima, ilustra perfeitamente a aplicação da regra de três composta, mostrando como lidar com múltiplas grandezas e suas relações de proporcionalidade. A organização em uma tabela facilita a visualização das relações e a montagem da proporção para a resolução.
Vimos que a regra de três simples, apesar de parecer simples à primeira vista, é uma ferramenta poderosa e versátil com aplicações em diversas áreas. Dominar a distinção entre regra de três direta e inversa, assim como os métodos de resolução passo a passo, é crucial para resolver problemas de proporcionalidade com eficiência e segurança. Com prática e entendimento dos conceitos, você estará apto a enfrentar desafios matemáticos com mais confiança e precisão.
Lembre-se: a prática leva à perfeição!

