A Trigonometria Tem Importantes Aplicações Como Por Exemplo Nas Engenharias, uma verdade que se revela através da sua capacidade de desvendar os segredos dos ângulos e das relações entre os lados de figuras geométricas. Desde a construção de pontes e edifícios imponentes até a criação de máquinas complexas e a exploração do espaço, a trigonometria é a linguagem matemática que permite aos engenheiros dar vida a ideias inovadoras e desafiadoras.
A trigonometria, com suas funções seno, cosseno e tangente, permite calcular distâncias, alturas, áreas e ângulos com precisão, tornando-se um instrumento fundamental para a realização de projetos de engenharia em diversas áreas, como civil, mecânica, elétrica e aeroespacial. A sua aplicação abrange desde a análise de estruturas e o cálculo de forças em sistemas mecânicos até a compreensão de sinais periódicos em circuitos elétricos e a determinação de trajetórias de foguetes durante o lançamento.
A Importância da Trigonometria nas Engenharias
A trigonometria é um ramo da matemática que estuda as relações entre os ângulos e os lados de triângulos. É uma ferramenta essencial para engenheiros de diversas áreas, pois permite a resolução de problemas complexos relacionados a geometria, medidas e cálculos de grandezas.
A Trigonometria como Base para a Compreensão de Figuras Geométricas
A trigonometria é fundamental para a compreensão de ângulos e relações entre lados em figuras geométricas. As funções trigonométricas, como seno, cosseno e tangente, permitem calcular os lados e ângulos de triângulos, bem como as relações entre eles. Essa compreensão é crucial para a resolução de problemas em diversas áreas da engenharia, como a determinação de distâncias, alturas, áreas e volumes.
Aplicações da Trigonometria em Cálculos de Distâncias, Alturas e Áreas
A trigonometria é amplamente utilizada para calcular distâncias, alturas e áreas em projetos de engenharia. Por exemplo, engenheiros civis utilizam a trigonometria para calcular a inclinação de rampas, a altura de edifícios e a distância entre pontos em um terreno.
Engenheiros mecânicos utilizam a trigonometria para calcular a força e o torque em sistemas de engrenagens e mecanismos.
Exemplos Práticos de Aplicações da Trigonometria em Diferentes Áreas da Engenharia
- Engenharia Civil:Cálculo da inclinação de rampas, determinação do ângulo de inclinação de telhados, dimensionamento de vigas e pilares, projetos de pontes e estradas.
- Engenharia Mecânica:Análise de movimentos de máquinas e mecanismos, cálculo de forças e momentos em estruturas mecânicas, projeto de sistemas de engrenagens e rolamentos.
- Engenharia Elétrica:Análise de circuitos elétricos e sinais periódicos, cálculo de impedância e potência em circuitos elétricos, projeto de sistemas de transmissão de energia e telecomunicações.
- Engenharia Aeroespacial:Cálculo da trajetória de foguetes durante o lançamento, determinação da altitude e velocidade de aviões em voo, projeto de satélites e sistemas de navegação.
Aplicações da Trigonometria em Projetos de Engenharia Civil
A trigonometria é uma ferramenta essencial para engenheiros civis, sendo utilizada em diversas etapas de um projeto, desde o planejamento até a execução.
Cálculo da Inclinação de Rampas
Para calcular a inclinação de uma rampa, é necessário utilizar a tangente do ângulo de inclinação. A tangente é a razão entre o cateto oposto (altura da rampa) e o cateto adjacente (comprimento da rampa). Por exemplo, se a altura da rampa é de 1 metro e o comprimento é de 5 metros, a tangente do ângulo de inclinação é 1/5, o que corresponde a um ângulo de aproximadamente 11,3 graus.
Determinação do Ângulo de Inclinação de um Telhado
A trigonometria também é utilizada para determinar o ângulo de inclinação de um telhado em um projeto arquitetônico. O ângulo de inclinação é importante para garantir a resistência e a impermeabilidade do telhado. Para calcular o ângulo de inclinação, é necessário utilizar a tangente do ângulo, que é a razão entre a altura do telhado e a metade do comprimento da base do telhado.
Exemplos de Aplicações da Trigonometria em Projetos de Engenharia Civil
| Projeto | Aplicações da Trigonometria |
|---|---|
| Pontes | Cálculo do comprimento dos cabos de sustentação, determinação do ângulo de inclinação dos pilares, análise da estrutura da ponte sob diferentes condições de carga. |
| Edifícios | Cálculo da altura dos edifícios, determinação do ângulo de inclinação das paredes, análise da resistência da estrutura do edifício sob diferentes condições de vento e terremoto. |
| Estradas | Cálculo da inclinação das curvas, determinação do ângulo de inclinação das rampas, análise da geometria da estrada para garantir a segurança dos veículos. |
A Trigonometria na Engenharia Mecânica
A trigonometria é fundamental para a análise de movimentos de máquinas e mecanismos, cálculo de forças e momentos em estruturas mecânicas e projeto de sistemas de engrenagens e rolamentos.
Análise de Movimentos de Máquinas e Mecanismos
A trigonometria é utilizada para analisar o movimento de máquinas e mecanismos, como motores, engrenagens e sistemas de transmissão. As funções trigonométricas permitem calcular a posição, a velocidade e a aceleração de cada componente do mecanismo em função do tempo.
Essa análise é essencial para garantir o funcionamento adequado do mecanismo e otimizar seu desempenho.
Cálculo de Forças e Momentos em Estruturas Mecânicas
A trigonometria é aplicada para calcular forças e momentos em estruturas mecânicas, como vigas, pilares e chassis de veículos. As funções trigonométricas permitem determinar a direção e a intensidade das forças que atuam sobre a estrutura, bem como os momentos resultantes.
Essa análise é crucial para garantir a resistência e a estabilidade da estrutura.
Aplicações da Trigonometria em Projetos de Máquinas Simples e Complexas
A trigonometria é utilizada em projetos de máquinas simples, como alavancas e polias, para determinar a força necessária para levantar uma carga. Em projetos de máquinas complexas, como motores e turbinas, a trigonometria é utilizada para analisar o movimento de cada componente e calcular as forças que atuam sobre eles.
As aplicações da trigonometria em projetos de máquinas simples e complexas são essenciais para garantir o funcionamento adequado e a segurança dos equipamentos.
A Trigonometria na Engenharia Elétrica
A trigonometria é uma ferramenta essencial para engenheiros eletricistas, sendo utilizada em diversas áreas, como análise de circuitos elétricos, projeto de sistemas de transmissão de energia e telecomunicações.
Análise de Circuitos Elétricos e Sinais Periódicos
A trigonometria é utilizada para analisar circuitos elétricos e sinais periódicos, como ondas senoidais e ondas quadradas. As funções trigonométricas permitem representar os sinais elétricos em forma de ondas senoidais e calcular a amplitude, a frequência e a fase do sinal.
Essa análise é essencial para o projeto de sistemas de comunicação e controle.
Cálculo de Impedância e Potência em Circuitos Elétricos
A trigonometria é aplicada para calcular a impedância e a potência em circuitos elétricos. A impedância é a resistência total que um circuito oferece à passagem de corrente elétrica. A potência é a taxa de consumo de energia elétrica em um circuito.
As funções trigonométricas permitem calcular a impedância e a potência em função da frequência e da fase do sinal elétrico.
Exemplos de Aplicações da Trigonometria em Diferentes Áreas da Engenharia Elétrica
| Área | Aplicações da Trigonometria |
|---|---|
| Transmissão de Energia | Cálculo da impedância das linhas de transmissão, análise da potência transmitida, projeto de sistemas de proteção contra falhas. |
| Telecomunicações | Análise de sinais de rádio e televisão, projeto de antenas e sistemas de comunicação sem fio, modulação e demodulação de sinais. |
A Trigonometria na Engenharia Aeroespacial
A trigonometria é uma ferramenta essencial para engenheiros aeroespaciais, sendo utilizada em diversas áreas, como cálculo da trajetória de foguetes, determinação da altitude e velocidade de aviões em voo e projeto de satélites.
Cálculo da Trajetória de um Foguete Durante o Lançamento
A trigonometria é utilizada para calcular a trajetória de um foguete durante o lançamento. As funções trigonométricas permitem determinar a posição, a velocidade e a aceleração do foguete em função do tempo. Essa análise é essencial para garantir que o foguete atinja sua órbita desejada.
Determinação da Altitude e Velocidade de um Avião em Voo
A trigonometria é aplicada para determinar a altitude e a velocidade de um avião em voo. As funções trigonométricas permitem calcular a distância horizontal e vertical percorrida pelo avião, bem como a velocidade e a direção do voo. Essa análise é essencial para a navegação aérea e o controle de tráfego aéreo.
Exemplo de Cálculo da Distância entre Dois Satélites em Órbita
Para calcular a distância entre dois satélites em órbita, é necessário utilizar a lei dos cossenos. A lei dos cossenos é uma fórmula que relaciona os lados de um triângulo com o cosseno do ângulo oposto a um dos lados.
Se a distância entre os dois satélites é representada pelo lado c do triângulo, e as distâncias entre os satélites e um ponto de referência na Terra são representadas pelos lados a e b, então a lei dos cossenos pode ser escrita como: c^2 = a^2 + b^2 – 2ab*cos(C), onde C é o ângulo entre os lados a e b.
A trigonometria, portanto, emerge como uma ferramenta essencial para os engenheiros, proporcionando-lhes a capacidade de solucionar problemas complexos e de construir um mundo mais eficiente e tecnológico. É através da aplicação dos seus princípios que as ideias se transformam em realidade, e a engenharia avança, impulsionada pela precisão e pela beleza da matemática.
Top FAQs: A Trigonometria Tem Importantes Aplicações Como Por Exemplo Nas Engenharias
Quais são as principais funções trigonométricas?
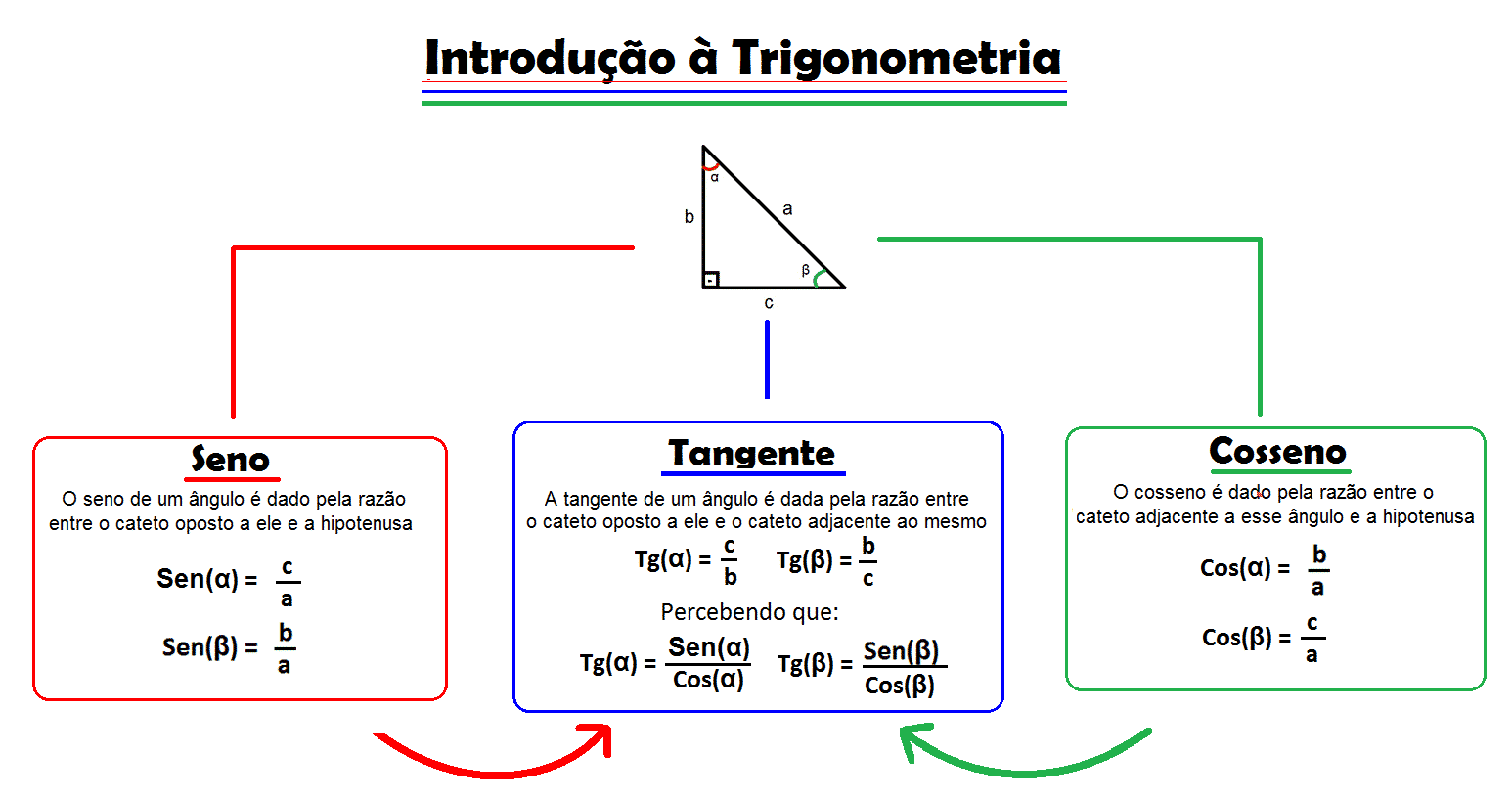
As principais funções trigonométricas são seno (sen), cosseno (cos) e tangente (tan). Cada uma delas relaciona um ângulo de um triângulo retângulo com a razão entre dois dos seus lados.
Como a trigonometria é utilizada na engenharia civil?
Na engenharia civil, a trigonometria é utilizada para calcular a inclinação de rampas, o ângulo de inclinação de telhados, a altura de edifícios, a distância entre pontos e o comprimento de vigas e pilares, entre outras aplicações.

